publications

2025

1. NeurIPS

   

   Pre-trained Large Language Models Learn to Predict Hidden Markov Models In-context

   Yijia Dai, Zhaolin Gao, Yahya Sattar, and 2 more authors

   Advances in Neural Information Processing Systems, 2025

   Abs PDF

   Hidden Markov Models (HMMs) are foundational tools for modeling sequential data with latent Markovian structure, yet fitting them to real-world data remains computationally challenging. In this work, we show that pre-trained large language models (LLMs) can effectively model data generated by HMMs via in-context learning (ICL)—their ability to infer patterns from examples within a prompt. On a diverse set of synthetic HMMs, LLMs achieve predictive accuracy approaching the theoretical optimum. We uncover novel scaling trends influenced by HMM properties, and offer theoretical conjectures for these empirical observations. We also provide practical guidelines for scientists on using ICL as a diagnostic tool for complex data. On real-world animal decision-making tasks, ICL achieves competitive performance with models designed by human experts. To our knowledge, this is the first demonstration that ICL can learn and predict HMM-generated sequences—an advance that deepens our understanding of in-context learning in LLMs and establishes its potential as a powerful tool for uncovering hidden structure in complex scientific data.

2. L4DC

   

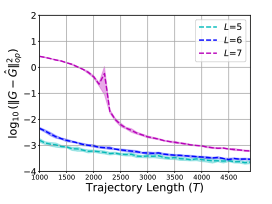   Finite Sample Identification of Partially Observed Bilinear Dynamical Systems

   Yahya Sattar, Yassir Jedra, Maryam Fazel, and 1 more author

   7th Annual Learning for Dynamics & Control Conference, 2025

   Abs PDF

   Bilinear dynamical systems are ubiquitous in many different domains and they can also be used to approximate more general control-affine systems. This motivates the problem of learning bilinear systems from a single trajectory of the system’s states and inputs. Under a mild marginal mean square stability assumption, we identify how much data is needed to estimate the unknown bilinear system up to a desired accuracy with high probability. Our sample complexity and statistical error rates are optimal in terms of the trajectory length, the dimensionality of the system and the input size. Our proof technique relies on an application of martingale small-ball condition. This enables us to correctly capture the properties of the problem, specifically our error rates do not deteriorate with increasing instability. Finally, we show that numerical experiments are well-aligned with our theoretical results.

3. Submission

   

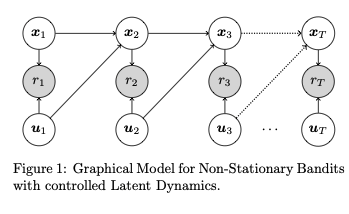   Explore-then-Commit for Nonstationary Linear Bandits with Latent Dynamics

   Sunmook Choi, Yahya Sattar, Yassir Jedra, and 2 more authors

   under Submission, 2025

   Abs PDF

   We study a nonstationary bandit problem where rewards depend on both actions and latent states, the latter governed by unknown linear dynamics. Crucially, the state dynamics also depend on the actions, resulting in tension between short-term and long-term rewards. We propose an explore-then-commit algorithm for a finite horizon T. During the exploration phase, random Rademacher actions enable estimation of the Markov parameters of the linear dynamics, which characterize the action-reward relationship. In the commit phase, the algorithm uses the estimated parameters to design an optimized action sequence for long-term reward. Our proposed algorithm achieves O(T^2/3) regret. Our analysis handles two key challenges: learning from temporally correlated rewards, and designing action sequences with optimal long-term reward. We address the first challenge by providing near-optimal sample complexity and error bounds for system identification using bilinear rewards. We address the second challenge by proving an equivalence with indefinite quadratic optimization over a hypercube, a known NP-hard problem. We provide a sub-optimality guarantee for this problem, enabling our regret upper bound. Lastly, we propose a semidefinite relaxation with Goemans-Williamson rounding as a practical approach.

4. CDC

   

   Sub-Optimality of the Separation Principle for Quadratic Control from Bilinear Observations

   Yahya Sattar, Sunmook Choi, Yassir Jedra, and 2 more authors

   2025 IEEE 64th Conference on Decision and Control (CDC), 2025

   Abs PDF

   We consider the problem of controlling a linear dynamical system from bilinear observations with minimal quadratic cost. Despite the similarity of this problem to standard linear quadratic Gaussian (LQG) control, we show that when the observation model is bilinear, neither does the Separation Principle hold, nor is the optimal controller affine in the estimated state. Moreover, the cost-to-go is non-convex in the control input. Hence, finding an analytical expression for the optimal feedback controller is difficult in general. Under certain settings, we show that the standard LQG controller locally maximizes the cost instead of minimizing it. Furthermore, the optimal controllers (derived analytically) are not unique and are nonlinear in the estimated state. We also introduce a notion of input-dependent observability and derive conditions under which the Kalman filter covariance remains bounded. We illustrate our theoretical results through numerical experiments in multiple synthetic settings.

5. ACC

   

   Learning Linear Dynamics from Bilinear Observations

   Yahya Sattar, Yassir Jedra, and Sarah Dean

   In 2025 American Control Conference (ACC), 2025

   Abs PDF

   We consider the problem of learning a realization of a partially observed dynamical system with linear state transitions and bilinear observations. Under very mild assumptions on the process and measurement noises, we provide a finite time analysis for learning the unknown dynamics matrices (up to a similarity transform). Our analysis involves a regression problem with heavy-tailed and dependent data. Moreover, each row of our design matrix contains a Kronecker product of current input with a history of inputs, making it difficult to guarantee persistence of excitation. We overcome these challenges, first providing a data-dependent high probability error bound for arbitrary but fixed inputs. Then, we derive a data-independent error bound for inputs chosen according to a simple random design. Our main results provide an upper bound on the statistical error rates and sample complexity of learning the unknown dynamics matrices from a single finite trajectory of bilinear observations.

6. CPAL

   

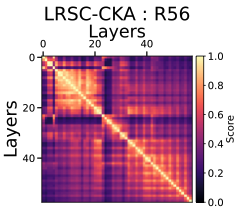   A Case Study of Low Ranked Self-Expressive Structures in Neural Network Representations

   Uday Singh Saini, William Shiao, Yahya Sattar, and 3 more authors

   In The Second Conference on Parsimony and Learning (Proceedings Track), 2025

   Abs PDF

   Understanding neural networks by studying their underlying geometry can help us understand their embedded inductive priors and representation capacity. Prior representation analysis tools like (Linear) Centered Kernel Alignment (CKA) offer a lens to probe those structures via a kernel similarity framework. In this work we approach the problem of understanding the underlying geometry via the lens of subspace clustering, where each input is represented as a linear combination of other inputs. Such structures are called self-expressive structures. In this work we analyze their evolution and gauge their usefulness with the help of linear probes. We also demonstrate a close relationship between subspace clustering and linear CKA and demonstrate its utility to act as a more sensitive similarity measure of representations when compared with linear CKA. We do so by comparing the sensitivities of both measures to changes in representation across their singular value spectrum, by analyzing the evolution of self-expressive structures in networks trained to generalize and memorize and via a comparison of networks trained with different optimization objectives. This analysis helps us ground the utility of subspace clustering based approaches to analyze neural representations and motivate future work on exploring the utility of enforcing similarity between self-expressive structures as a means of training neural networks.

2024

1. L4DC

   

   Random Features Approximation for Control-Affine Systems

   Kimia Kazemian, Yahya Sattar, and Sarah Dean

   In 6th Annual Learning for Dynamics & Control Conference, 2024

   Abs PDF

   Modern data-driven control applications call for flexible nonlinear models that are amenable to principled controller synthesis and realtime feedback. Many nonlinear dynamical systems of interest are control affine. We propose two novel classes of nonlinear feature representations which capture control affine structure while allowing for arbitrary complexity in the state dependence. Our methods make use of random features (RF) approximations, inheriting the expressiveness of kernel methods at a lower computational cost. We formalize the representational capabilities of our methods by showing their relationship to the Affine Dot Product (ADP) kernel proposed by Casta  neda et al. (2021) and a novel Affine Dense (AD) kernel that we introduce. We further illustrate the utility by presenting a case study of data-driven optimization-based control using control certificate functions (CCF). Simulation experiments on a double pendulum empirically demonstrate the advantages of our methods.

2023

1. TAC

   

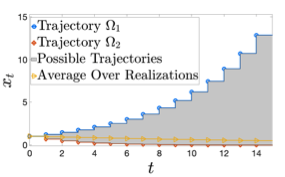   Identification and Adaptive Control of Markov Jump Systems: Sample Complexity and Regret Bounds

   Yahya Sattar, Zhe Du, Davoud Ataee Tarzanagh, and 3 more authors

   IEEE Transactions on Automatic Control (Submission), 2023

   Abs PDF

   Learning how to effectively control unknown dynamical systems is crucial for intelligent autonomous systems. This task becomes a significant challenge when the underlying dynamics are changing with time. Motivated by this challenge, this paper considers the problem of controlling an unknown Markov jump linear system (MJS) to optimize a quadratic objective. By taking a model-based perspective, we consider identification-based adaptive control of MJSs. We first provide a system identification algorithm for MJS to learn the dynamics in each mode as well as the Markov transition matrix, underlying the evolution of the mode switches, from a single trajectory of the system states, inputs, and modes. Through martingale-based arguments, sample complexity of this algorithm is shown to be O(1/sqrt(T)). We then propose an adaptive control scheme that performs system identification together with certainty equivalent control to adapt the controllers in an episodic fashion. Combining our sample complexity results with recent perturbation results for certainty equivalent control, we prove that when the episode lengths are appropriately chosen, the proposed adaptive control scheme achieves O(sqrt(T)) regret, which can be improved to O(polylog(T)) with partial knowledge of the system. Our proof strategy introduces innovations to handle Markovian jumps and a weaker notion of stability common in MJSs. Our analysis provides insights into system theoretic quantities that affect learning accuracy and control performance. Numerical simulations are presented to further reinforce these insights.

2022

1. JMLR

   

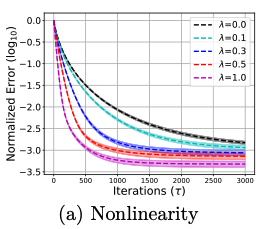   Non-asymptotic and Accurate Learning of Nonlinear Dynamical Systems

   Yahya Sattar and Samet Oymak

   Journal of Machine Learning Research, 2022

   Abs PDF

   We consider the problem of learning a nonlinear dynamical system governed by a nonlinear state equation h_t+1 = φ(h_t, u_t; θ) + w_t. Here θis the unknown system dynamics, h_t is the state, u_t is the input and w_t is the additive noise vector. We study gradient based algorithms to learn the system dynamics θfrom samples obtained from a single finite trajectory. If the system is run by a stabilizing input policy, then using a mixing-time argument we show that temporally-dependent samples can be approximated by i.i.d. samples. We then develop new guarantees for the uniform convergence of the gradient of the empirical loss induced by these i.i.d. samples. Unlike existing works, our bounds are noise sensitive which allows for learning the ground-truth dynamics with high accuracy and small sample complexity. When combined, our results facilitate efficient learning of a broader class of nonlinear dynamical systems as compared to the prior works. We specialize our guarantees to entrywise nonlinear activations and verify our theory in various numerical experiments.

2. CDC

   

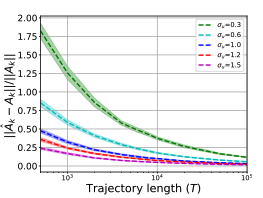   Finite Sample Identification of Bilinear Dynamical Systems

   Yahya Sattar, Samet Oymak, and Necmiye Ozay

   In 2022 IEEE 61st Conference on Decision and Control (CDC), 2022

   Abs PDF

   Bilinear dynamical systems are ubiquitous in many different domains and they can also be used to approximate more general control-affine systems. This motivates the problem of learning bilinear systems from a single trajectory of the systems states and inputs. Under a mild marginal mean-square stability assumption, we identify how much data is needed to estimate the unknown bilinear system up to a desired accuracy with high probability. Our sample complexity and statistical error rates are optimal in terms of the trajectory length, the dimensionality of the system and the input size. Our proof technique relies on an application of martingale small-ball condition. This enables us to correctly capture the properties of the problem, specifically our error rates do not deteriorate with increasing instability. Finally, we show that numerical experiments are well-aligned with our theoretical results.

3. ACC

   

   Data-Driven Control of Markov Jump Systems: Sample Complexity and Regret Bounds

   Zhe Du, Yahya Sattar, Davoud Ataee Tarzanagh, and 3 more authors

   In 2022 American Control Conference (ACC), 2022

   Abs PDF

   Learning how to effectively control unknown dynamical systems from data is crucial for intelligent autonomous systems. This task becomes a significant challenge when the underlying dynamics are changing with time. Motivated by this challenge, this paper considers the problem of controlling an unknown Markov jump linear system (MJS) to optimize a quadratic objective in a data-driven way. By taking a model-based perspective, we consider identification-based adaptive control for MJS. We first provide a system identification algorithm for MJS to learn the dynamics in each mode as well as the Markov transition matrix, underlying the evolution of the mode switches, from a single trajectory of the system states, inputs, and modes. Through mixing-time arguments, sample complexity of this algorithm is shown to be O(1/sqrt(T)). We then propose an adaptive control scheme that performs system identification together with certainty equivalent control to adapt the controllers in an episodic fashion. Combining our sample complexity results with recent perturbation results for certainty equivalent control, we prove that when the episode lengths are appropriately chosen, the proposed adaptive control scheme achieves O(sqrt(T)) regret. Our proof strategy introduces innovations to handle Markovian jumps and a weaker notion of stability common in MJSs. Our analysis provides insights into system theoretic quantities that affect learning accuracy and control performance. Numerical simulations are presented to further reinforce these insights.

4. ACC

   

   Certainty Equivalent Quadratic Control for Markov Jump Systems

   Yahya Sattar, Zhe Du, Davoud Ataee Tarzanagh, and 3 more authors

   2022 American Control Conference (ACC), 2022

   Abs PDF

   Real-world control applications often involve complex dynamics subject to abrupt changes or variations. Markov jump linear systems (MJS) provide a rich framework for modeling such dynamics. Despite an extensive history, theoretical understanding of parameter sensitivities of MJS control is somewhat lacking. Motivated by this, we investigate robustness aspects of certainty equivalent model-based optimal control for MJS with quadratic cost function. Given the uncertainty in the system matrices and in the Markov transition matrix is bounded by and respectively, robustness results are established for (i) the solution to coupled Riccati equations and (ii) the optimal cost, by providing explicit perturbation bounds which decay as O(ε+ η)and O((ε+ η)2) respectively.

2021

1. ICASSP

   

   Estimation of Groundwater Storage Variations in Indus River Basin Using GRACE Data

   Yahya Sattar and Zubair Khalid

   In IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2021

   Abs PDF

   The depletion and variations of groundwater storage (GWS) are of critical importance for sustainable groundwater management. In this work, we use Gravity Recovery and Climate Experiment (GRACE) to estimate variations in the terrestrial water storage (TWS) and use it in conjunction with the Global Land Data Assimilation Sys tem (GLDAS) data to extract GWS variations over time for Indus river basin (IRB). We present a data processing framework that pro cesses and combines these data-sets to provide an estimate of GWS changes. We also present the design of a band-limited optimally concentrated window function for spatial localization of the data in the region of interest. We construct the so-called optimal window for the IRB region and use it in our processing framework to ana lyze the GWS variations from 2005 to 2015. Our analysis reveals the expected seasonal variations in GWS and signifies groundwater depletion on average over the time period. Our proposed process ing framework can be used to analyze spatio-temporal variations in TWSandGWSforany region of interest.

2. ICoDT2

   

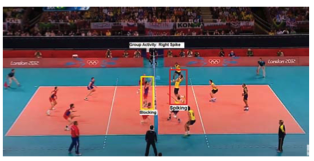   Group Activity Recognition in Visual Data: A Retrospective Analysis of Recent Advancements

   Shoaib Sattar, Yahya Sattar, Muhammad Shahzad, and 1 more author

   In International Conference on Digital Futures and Transformative Technologies (ICoDT2), 2021

   Abs PDF

   Human-activity recognition has gained significant attention recently within the computer vision and machine learning community, due to its applications in diverse fields such as health, entertainment, visual surveillance and sports analytics. An important sub-category of human-activity recognition is group activity recognition (GAR) where a group of individuals is involved in an activity. The main challenge in such recognition tasks is to learn the relationship between a group of individuals in a scene and its evolution over time. Recently, many techniques based on deep networks and graphical models have been proposed for group activity recognition. In this paper, we critically analyze the state-of-the-art (SOTA) techniques for group activity recognition. We propose a new taxonomy for categorizing the SOTA techniques conducted in the field of group activity recognition and divide the existing literature into different subcategories. We also identify the available datasets and the existing research challenges for GAR.

2020

1. TSP

   

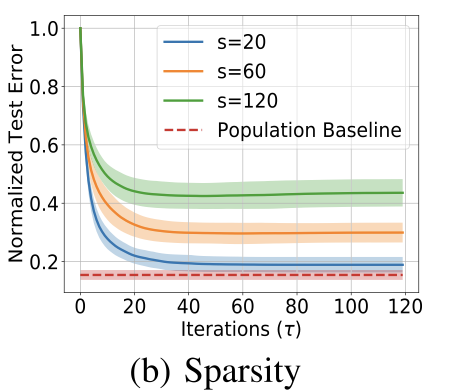   Quickly Finding the Best Linear Model in High Dimensions via Projected Gradient Descent

   Yahya Sattar and Samet Oymak

   IEEE Transactions on Signal Processing, 2020

   Abs PDF

   We study the problem of finding the best linear model that can minimize least-squares loss given a dataset. While this problem is trivial in the low-dimensional regime, it becomes more interesting in high-dimensions where the population minimizer is assumed to lie on a manifold such as sparse vectors. We propose projected gradient descent (PGD) algorithm to estimate the population minimizer in the finite sample regime. We establish linear convergence rate and data-dependent estimation error bounds for PGD. Our contributions include: 1) The results are established for heavier tailed subexponential distributions besides subgaussian and allows for an intercept term. 2) We directly analyze the empirical risk minimization and do not require a realizable model that connects input data and labels. The numerical experiments validate our theoretical results.

2. preprint

   

   Exploring Weight Importance and Hessian Bias in Model Pruning

   Mingchen Li, Yahya Sattar, Christos Thrampoulidis, and 1 more author

   arXiv preprint, 2020

   Abs PDF

   Model pruning is an essential procedure for building compact and computationally-efficient machine learning models. A key feature of a good pruning algorithm is that it accurately quantifies the relative importance of the model weights. While model pruning has a rich history, we still don’t have a full grasp of the pruning mechanics even for relatively simple problems involving linear models or shallow neural nets. In this work, we provide a principled exploration of pruning by building on a natural notion of importance. For linear models, we show that this notion of importance is captured by covariance scaling which connects to the well-known Hessian-based pruning. We then derive asymptotic formulas that allow us to precisely compare the performance of different pruning methods. For neural networks, we demonstrate that the importance can be at odds with larger magnitudes and proper initialization is critical for magnitude-based pruning. Specifically, we identify settings in which weights become more important despite becoming smaller, which in turn leads to a catastrophic failure of magnitude-based pruning. Our results also elucidate that implicit regularization in the form of Hessian structure has a catalytic role in identifying the important weights, which dictate the pruning performance.

2019

1. CAMSAP

   

   A Simple Framework for Learning Stabilizable Systems

   Yahya Sattar and Samet Oymak

   In IEEE 8th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), 2019

   Abs PDF

   We propose a framework for learning discrete time stabilizable systems governed by nonlinear state equation h_t+1 = φ(h_t, u_t; θ). Here θis the possibly unknown system dynamics, h_t is the state and u_t is the input vector. We utilize gradient descent to learn the system dynamics θfrom a finite trajectory. We show that gradient descent linearly converges to the ground truth dynamics with good sample complexity when system satisfies certain properties. The proposed framework allows for simultaneously learning and controlling the system and establishes a simple connection between classical supervised learning and temporally-dependent problems via mixing-time arguments. Numerical experiments verify our theoretical findings.

2. ICASSP

   

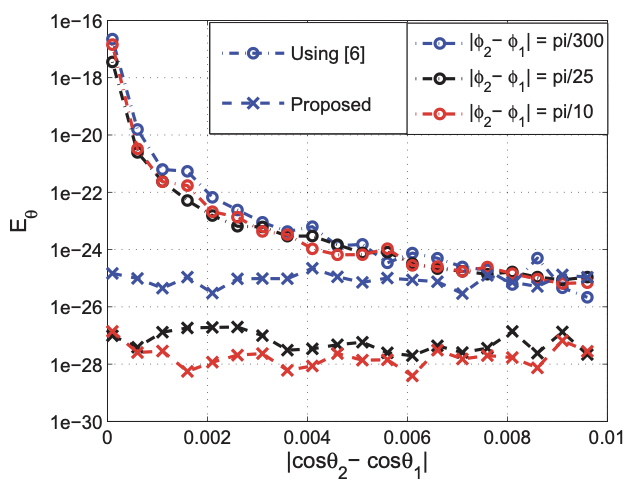   Accurate Reconstruction of Finite Rate of Innovation Signals on the Sphere

   Yahya Sattar, Zubair Khalid, and Rodney A Kennedy

   In IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2019

   Abs PDF

   We propose a method for the accurate and robust reconstruction of the non-bandlimited finite rate of innovation signals on the sphere. For signals consisting of a finite number of Dirac functions on the sphere, we develop an annihilating filter based method for the accurate recovery of parameters of the Dirac functions using a finite number of observations of the bandlimited signal. In comparison to existing techniques, the proposed method enables more accurate reconstruction primarily due to the better conditioning of systems involved in the recovery of parameters. In order to reconstruct K Diracs on the sphere, the proposed method requires samples of the signal bandlimited in the spherical harmonic (SH) domain at SH degree equal or greater than K + sqrt(K + 1/4) - 1/2. In comparison to the existing state-of-the-art technique, the required bandlimit, and consequently the number of samples, of the proposed method is (approximately) the same. We also conduct numerical experiments to demonstrate that the proposed technique is more accurate than the existing methods by a factor of 10^7 or more for 2 ≤K ≤20.

2017

1. ICASSP

   

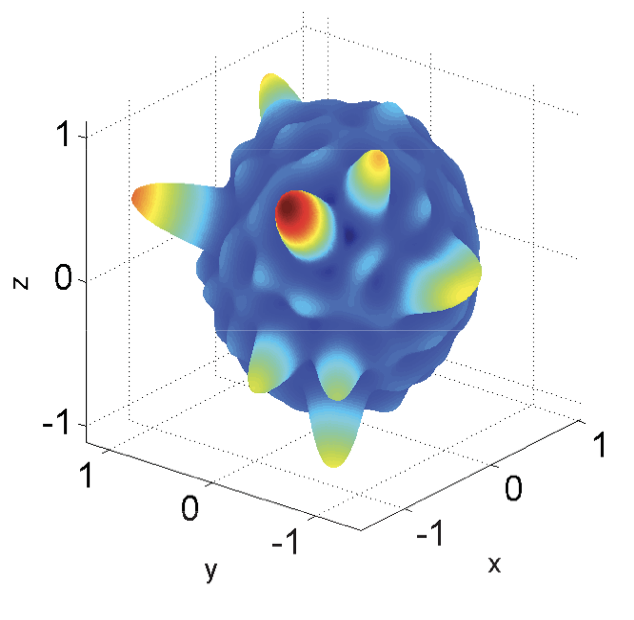   Robust Reconstruction of Spherical Signals with Finite Rate of Innovation

   Yahya Sattar, Zubair Khalid, and Rodney A Kennedy

   In IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2017

   Abs PDF

   We develop a robust method for the accurate reconstruction of non-bandlimited finite rate of innovation signals composed of finite number of Diracs. For the recovery of parameters of K Diracs defining the signal, the proposed method requires more than (K + sqrt(K))^2 samples of the signal band-limited in harmonic domain such that the spherical harmonic transform can be computed using the samples. In comparison with the existing methods, the proposed method is robust in a sense that it does not require all Diracs to have distinct colatitude parameter. We first estimate the N number of Diracs which do not have distinct colatitude parameter. Once N is determined, the proposed method requires, at most, (N^2+N)/2 + 1 unique and intelligently chosen rotations of the signal to recover all parameters accurately. We also provide illustrations to demonstrate the accurate reconstruction using the proposed method.